[수학] -1*-1=1인 이유는
음수와 음수를 곱하면 양수가 된다는데, 그냥 그렇다고 외우기만 했을 뿐, 그 이유를 생각해 보지 못했다. 음수끼리 더하면 여전히 음수인데 왜 곱하면 양수가 될까? 생각해 보면, 곱이 양수가 되는 것은커녕 음수끼리 어떻게 곱할 수 있는지도 이해하기 어렵다. 음수와 음수의 곱은 도대체 무엇일까?
음수를 이해할 수 있는 쉬운 방법 가운데 하나는 아마도 금전적 이익을 양, 금전적 손실을 음으로 생각하는 방식일 것이다. 그런데 이 방식은 음수의 덧뺄셈을 설명하는 데는 좋지만, 곱셈이나 나눗셈을 다루는 데는 오히려 방해가 된다. 일례로, 소설 <적과 흑>으로 유명한 프랑스의 작가 스탕달(Stendhal, 1783-1842)은 자전적 소설에서, “1만 프랑의 빚과 5백 프랑의 빚을 곱하면 어떻게 5백만 프랑의 이익이 된다는 말인가?”라고 썼다. 음수와 음수의 곱이 양수인 것을 이해할 수 없다는 것이다. 당대의 지식인 가운데 한 명인 스탕달이 이 정도였으니, 음수에 음수를 곱해서 양수가 된다는 사실을 선뜻 받아들이지 못하는 사람들이 많았음을 짐작할 수 있다. 사실 무리수보다 음수가 더 늦게 발견됐으며, 음수의 연산을 보편적으로 받아들인 것이 무리수를 받아들인 것보다 나중인 것을 보면, 음수에 대한 거부감 내지는 공포감이 얼마나 심했는지 알 만하다. 희대의 천재로 손꼽히는 파스칼(Blaise Pascal, 1623-1662)조차 “놀랍게도, 아무것도 없는 상태에서 4개를 없애도 여전히 아무것도 없다는 사실을 이해하지 못하는 사람들이 있다”라고 자신의 책에 써놓을 정도였다.
양수와 음수의 모델 : 빚과 이익‘인간은 생각하는 갈대’라고 말한, ‘파스칼의 원리’를 발견한, 세계에서 처음으로 계산기를 만든 그 파스칼이 말이다. 음수 곱하기 음수가 양수라는 것은 문헌 상으로는 7세기 인도의 수학자 브라흐마굽타(Brahmagupta, 598–668)가 처음 밝혔다. 그렇지만, -3이 2보다 작은데 어떻게 -3의 제곱이 2의 제곱보다 크냐는 반론이 1000년도 더 지난 18세기 유럽에서 버젓이 상식처럼 통용되기도 하였으니, 음수에 음수를 곱한 것이 양수라는 사실에 대한 저항이 만만치 않았음을 알 수 있다. 오늘날처럼 경제나 날씨 등에서 음수의 개념이 일상화된 사회에서는 이러한 저항이 훨씬 덜한 편이지만, 여전히 음수를 처음 배우는 사람들이나 배운지 오랜 사람들에게는 낯설게 느껴지는 것도 사실이다.
스탕달의 예에서처럼 음수와 양수는 “빚”과 “이익”이라는 모델이 있다. 양수를 이익으로 생각하고 음수를 빚으로 생각하면, 이 모델은 양수의 덧셈과 뺄셈을 모두 설명할 수 있기 때문에 매우 좋은 모델이라 할 수 있다. 예를 들어 양수를 더하는 것은 이익이 늘어나는 것이고, 음수를 더하는 것은 이익이 줄어드는 것으로 생각하는 것이다. (이익이 0보다 작으면 빚으로 해석한다.) 인간은 한번 성공한 방법을 상황이 달라지더라도 적용하려는 경향이 있어서, 양수와 음수에 대한 연산을 할 때면 으레 빚과 이익을 생각하기 마련이다. 따라서 음수를 곱해서 양수라는 것을 빚과 빚을 곱해서 이익이라는 모델로 이해하려 시도하는 것도 자연스러운 현상이다. 왜 이 모델이 곱셈을 다룰 때는 잘 작동하지 않는 것일까?
빚과 이익 모델을 써서 곱하기를 하려고 하면, 양수 곱하기 양수를 설명할 때부터 벌써 삐걱거리기 시작한다. 이 모델대로라면 ‘이익’에 ‘이익’을 곱하면 ‘이익’이라는 말인데 과연 그럴까? 100원짜리가 10개 있으면 1,000원(100 × 10 = 1,000)이므로 양수를 곱하면 양수라는 것은 얼핏 보면 그럴듯한 설명처럼 보인다. 그런데 잘 들여다보면 앞의 100의 단위는 ‘원’이지만, 뒤의 10은 단위가 ‘개수’임을 알 수 있다. 앞의 100원은 ‘이익’이라 불러도 괜찮지만, 뒤의 10개는 ‘이익’이라고 해석하기 곤란한 것이다. 따라서 빚에 빚을 곱하는 것은 고사하고, 이익에 이익을 곱한다는 것부터가 어불성설임을 알 수 있다.
‘이익의 곱은 이익’이라는 말은 틀린 ‘해석’이지만, 빚과 이익 모델로도 일단 양수 곱하기 양수가 양수라는 것을 설명하는 데는 별 문제가 없다. 한편, 이 모델로 음수 곱하기 양수가 음수라는 것도 설명할 수 있다. 예를 들어, 천 원을 빚진 사람이 열 명이면, 전체 빚이 만원임을 안다. 식으로 쓰면 아래와 같이 나타낼 수 있다.
이와 같이 음수 곱하기 양수와 양수 곱하기 음수가 음수라는 것을 설명할 수 있기 때문에 (역시 ‘빚 곱하기 이익이 빚’이라는 얘기는 아니다) 곱셈일 때도 완전히 폐기처분하기에 아까운 모델이기는 하다. 그렇지만 이 모델은 ‘음수 곱하기 음수’를 잘 설명할 수 없다는 것이 결정적 약점이다. 무엇보다 사람수나 개수에는 음수가 없기 때문이다. 물론 이해해 볼 방법이 없는 것은 아닌데, 조금 뒤로 미루자.
위의 곱셈표를 보자. 가로줄을 보면, 곱해지는 수를 하나씩 줄임에 따라 곱셈의 결과도 일정하게 변한다. 세로줄을 보면 곱하는 수를 하나씩 줄임에 따라 역시 일정하게, 첫 번째 세로줄은 2씩 줄고, 두 번째 줄은 1씩 줄고, 세 번째 줄은 0으로 변함이 없고, 네 번째 줄은 1씩 늘고, 다섯 번째 줄은 2씩 늘고 있다. 따라서 다음 가로줄을 만들면 아래와 같이 되어야 원래의 규칙이 유지된다.
이로부터 음수에 음수를 곱하면 양수가 되는 것이 매우 자연스럽다는 것을 알 수 있다. (원한다면두어 줄 더 계산해도 좋다.)
음수를 다루는 기본적인 방식 가운데 하나는 수에 방향성을 부여하는 것이다. 양수와 음수를 양의 방향과 음의 방향의 두 가지로 생각하면 모델링 하기에 편리하다. 우리가 잘 알고 있는 수직선(數直線)이 바로 그것이다. 수직선에서 3과 -3은 기준점이 되는 원점에서 같은 거리(양)만큼 떨어져 있지만 방향이 서로 반대여서 다른 수가 된다. 사실 수직선 모델이 나온 이후에야 비로소 파스칼처럼 음수의 존재 자체를 부정하는 경향이 사라졌다. 이 수직선 모델에서 2에 3을 곱하는 것은 2를 3번 더하는 것이므로, 수직선의 0에서 양의 방향으로 2칸씩 3번 이동한 결과로 생각할 수 있다.
같은 방식으로 2에 -3을 곱하는 것은 반대 방향으로 2칸씩 3번, 즉 -2만큼 움직이는 과정을 3번 반복한 것으로 생각할 수 있다. 즉, -2에 3을 곱하는 것과 마찬가지로 생각할 수 있다.
이제(-2)×(-3)을 생각해 보면 -2의 반대 방향으로 3번 움직이는 것에 해당하고, 이것은 2를 3번 더한 것과 같아지므로,(-2)×(-3) = 6이 된다.
빚과 이익 모델로도 음수의 곱을 설명할 수 있다. 양수만 더하고 빼던 것을, 음수도 더하고 빼는 것으로 확장하는 것이다. 음수를 더하는 것은 빚이 늘어난다, 이익이 줄어든다는 뜻으로 해석하고, 음수를 뺀다는 것은 빚이 줄어든다, 즉, 이익이 늘어난다는 뜻으로 해석하는 것이 합리적이다. 특히 a가 양수일 때,-a를 뺀다는 것은 a만큼의 빚(즉, -a)이 줄었다는 뜻이므로, a만큼의 이익이 늘어났다는 뜻이다. 즉,-(-a) = a인 것이다. 또한 빚과 이익 모델에서 a와 b가 양수일 때(-a) × b = -(a × b) = a × (-b)라는 것은 수긍할 수 있을 것이다. 음수의 곱셈이 기존의 셈법과 어울리려면 저 식이b가 음수일 때도 (혹은 0일 때도) 성립하는 것이 바람직할 것이다. 따라서 b가 음수일 때b = -c로 나타내면, c는 양수이고 (-a) × (-c) = a ×(-(-c)) = a × c여야만 한다.즉, 음수 곱하기 음수는 양수가 되는 것이 합리적이다.
음수와 음수의 곱이 양수임을 여러가지로 ‘설명’했지만, 엄밀한 증명이라고 하기는 어렵다. 예를 들어 -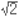
와 -
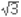의 곱이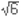 
임을 위의 설명을 써서 보이기 힘든데, 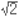번, 혹은 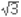개 같은 것을 생각할 수 없기 때문이다. 엄밀한 증명을 위해서는 0이 덧셈의 항등원이라는 것과, 덧셈의 결합법칙, 덧셈과 곱셈 사이의 분배법칙을 이용해여 (-a) × (-b) = ab를 증명할 수 있다. 먼저 음수와 음수의 곱 가운데 가장 간단한 (-1) × (-1) = 1을 연습 삼아 풀어보자. 0 = 1 + (-1)임은 알고 있다. 양변에 -1을 곱하고 분배법칙을 적용하면, 아래와 같다.
1 × (-1) = -1이므로 위의 식은 0=-1+(-1)×(-1) 이 된다. 이제 양변에 1을 더하면 결과가 나온다.
그럼, 이제 일반적인 음수와 음수의 곱에 대해서도 증명해 보겠다. 먼저 0 × b = 0 이라는 것을 증명한다. 0이 만약 3개 있다면 0 × 3 = 0 + 0 + 0 = 0 이니까 이런 것은 쉽다. 하지만 0에다 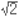를 곱한 것도 이렇게 생각할 수 있을까? 0이 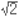번 있다는 것은 상상할 수 없다. 그래서 증명을 하는 것이다. 0 × b = 0의 증명은 다음과 같다.
a ×0 = 0인 것도 마찬가지로 똑같이 보일 수 있다. 이제 본격적으로(-a) × (-b) = ab를 증명하겠다. 그 증명은 아래와 같다.
이제 원하는 사실, (-a) × (-b) = ab의 증명이 끝났다.
관련링크 : [오늘의 과학] "-1 x -1 = 1 ?" 수학자 박부성님이 지식iN에 묻습니다.
관련링크 : 오늘의 과학 저자와의 질의응답 전체보기
출처 - http://navercast.naver.com/contents.nhn?rid=22&contents_id=106